안녕하세요~👋
오늘도 공부하는 무럭무럭 ✨성장몬✨ 입니다.
지난 Database 포스팅에 시간복잡도를 고려해서 문제를 푸는 분들이 있어
더 열심히 해야겠다고 다짐했었는데요!
시간복잡도를 고려하려면~
시간복잡도가 뭔지 알아야겠죠?! 🤭
마침 관련 강의를 발견해서 듣고서 포스팅해 봅니다^_^*
같이 성장하고 싶다면~?
인프런 > Do it! 알고리즘 코딩테스트 with JAVA > 섹션 0.코딩테스트 준비하기 > 시간복잡도
[TOC]
01 어떤 알고리즘으로 풀어야 할까?
ㅡ 알고리즘 선택의 기준이 되는 시간 복잡도
코딩 테스트의 핵심 중 하나는 문제마다 주어진 시간 복잡도를 고려해
적절한 알고리즘을 선택하는 것입니다.
처음에 알고리즘을 잘못 선택하면 아무리 코드를 잘 짜려고 노력해도
좋은 결과를 거두기 어려우니까요.
문제를 본격적으로 풀어 보기 전에 시간 복잡도를 표기하는 방법과
활용하는 방법을 익혀 보겠습니다.
01-1 시간 복잡도 표기법 알아보기
알고리즘에서 시간 복잡도는 주어진 문제를 해결하기 위한 연산 횟수를 말합니다. 일반적으로 수행 시간은 1억 번의 연산을 1초의 시간으로 간주하여 예측합니다.
💙 시간 복잡도 정의하기
실제 시간 복잡도를 정의하는 3가지 유형은 다음과 같습니다.
시간 복잡도 유형
- 빅-오메가(Ω(n)): 최선일 때(best case)의 연산 횟수를 나타낸 표기법
- 빅-세타(Θ(n)): 보통일 때(average case)의 연산 횟수를 나타낸 표기법
- 빅-오(O(n)): 최악일 때(worst case)의 연산 횟수를 나타낸 표기법
다음은 0~99 사이의 무작윗값을 찾아 출력하는 코드입니다. 빅-오메가 표기법(Ω(n))의 시간 복잡도는 1번, 빅-세타 표기법(Θ(n))의 시간 복잡도는 2/N번, 빅-오 표기법(O(n))의 시간 복잡도는 N번입니다.
시간 복잡도 예제 코드
1
2
3
4
5
6
7
8
9
10
11
12
public class timeComplexExample1 {
public static void main(String[] args) {
// 1~100 사이 값 랜덤 선택
int findNumber = (int)(Math.random() * 100);
for(int i= 0; i < 100; i++) {
if(i == findNumber){
System.out.print(i);
break;
}
}
}
}
💙 코딩 테스트에서는 어떤 시간 복잡도 유형을 사용해야 할까?
코딩 테스트에서는 빅-오 표기법(Ο(n))을 기준으로 수행 시간을 계산하는 것이 좋습니다. 실제 테스트에서는 1개의 테스트 케이스로 합격, 불합격을 결정하지 않습니다. 응시자가 작성한 프로그램으로 다양한 테스트 케이스를 수행해 모든 케이스를 통과해야만 합격으로 판단하므로 시간 복잡도를 판단할 때는 최악일 때 worst case를 염두에 둬야 합니다.
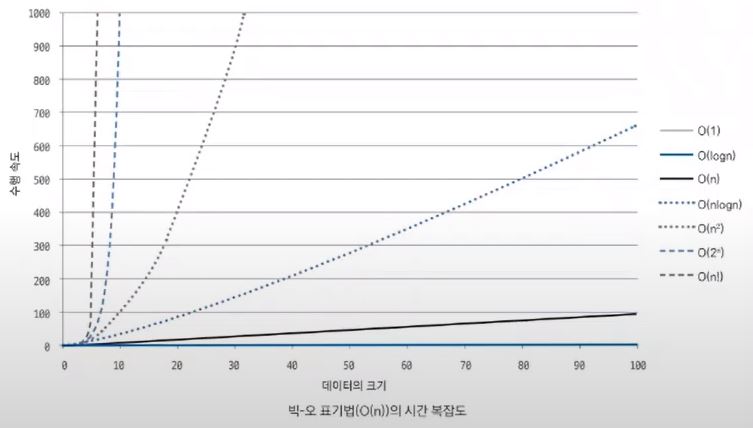
다음은 빅-오 표기법(Ο(n))으로 표현한 시간 복잡도 그래프입니다. 각각의 시간 복잡도는 데이터 크기(N)의 증가에 따라 성능(수행 시간)이 다르다는 것을 확인할 수 있습니다.
다음 절에서는 이러한 내용을 바탕으로 시간 복잡도의 개념을 코딩 테스트에 어떻게 활용해야 하는지 알아보겠습니다.
01-2 시간 복잡도 활용하기
💙 알고리즘 선택의 기준으로 사용하기
우리가 이 책에서 정렬 부분의 학습을 완료했고, 버블 정렬과 병합 정렬의 시간 복잡도를 각각 Ο(n²), Ο(nlogn)이라고 알고 있다고 가정하고 다음 문제를 예로 들어 설명하겠습니다.
문제 000 🎁 수 정렬하기
N개의 수가 주어졌을 때 이를 오름차순 정렬하는 프로그램을 작성하시오.
- 시간 제한 2초
- 백준 온라인 저지 2750번
📥 입력
1번째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000), 2번재 줄부터는 N개의 줄에 숫자가 주어진다. 이 수는 절댓값이 1,000,000보다 작거나 같은 정수다. 수는 중복되지 않는다.
📤 출력
1번째 줄부터 N개의 줄에 오름차순 정렬한 결과를 1줄에 1개씩 출력한다.
예제 입력 1
1 2 3 4 5 6
5 5 2 3 4 1
예제 출력 1
1 2 3 4 5
1 2 3 4 5
시간 제한이 2초이므로 이 조건을 만족하려면 2억 번 이하의 연산 횟수로 문제를 해결해야 합니다. 따라서 문제에서 주어진 시간 제한과 데이터 크기를 바탕으로 어떤 정렬 알고리즘을 사용해야 할 것인지를 판단할 수 있습니다.
✅ 연산 횟수는 1초에 1억 번 연산하는 것을 기준으로 생각합니다.
✅ 시간 복잡도는 항상 최악일 때, 즉 데이터의 크기가 가장 클 때를 기준으로 합니다.
연산 횟수 계산 방법
- 연산 횟수 = 알고리즘 시간 복잡도 X 데이터의 크기
위 공식을 대입해 각 알고리즘이 이 문제에 적합한지 판단해 보겠습니다.
알고리즘 적합성 평가
버블 정렬 = (1,000,000)² = 1,000,000,000,000 > 200,000,000 → 부적합 알고리즘
병합 정렬 = 1,000,000log(1,000,000) = 약 20,000,000 < 200,000,000 → 적합 알고리즘
문제에 주어진 시간 제한이 2초이므로 연산 횟수 2억 번 안에 원하는 답을 구해야 합니다. 버블 정렬은 약 10억 번의 연산 횟수가 필요하므로 이 문제를 풀기에 적합한 알고리즘이 아니라고 판단할 수 있습니다. 병합 정렬을 약 2,000만 번의 연산 횟수로 답을 구할 수 있으므로 문제를 풀기에 적합한 알고리즘이라고 판단할 수 있습니다.
이와 같이 시간 복잡도 분석으로 문제에서 사용할 수 있는 알고리즘을 선택할 수 있고, 이 범위를 바탕으로 문제의 실마리를 찾을 수 있습니다. 즉, 데이터의 크기(N)를 단서로 사용해야하는 알고리즘을 추측해 볼 수 있습니다.
💙 시간 복잡도를 바탕으로 코드 로직 개선하기
시간 복잡도는 작성한 코드의 비효율적인 로직을 개선하는 바탕으로도 사용할 수 있습니다. 이 부분을 활용하려면 가장 먼저 코드의 시간 복잡도를 도출할 수 있어야 합니다. 시간 복잡도를 도출하려면 다음 2가지 기준을 고려해야 합니다.
시간 복잡도 도출 기준
① 상수는 시간 복잡도 계산에서 제외한다.
② 가장 많이 중첩된 반복문의 수행 횟수가 시간 복잡도의 기준이 된다.
코드를 예로 들어 설명하겠습니다.
연산 횟수가 N인 경우
1
2
3
4
5
6
7
8
9
public class 시간복잡도_판별원리1 {
public static void main(String[] args) {
int N = 100000;
int cnt = 0;
for (int i = 0; i < N; i++) {
System.out.println("연산 횟수:" + cnt++);
}
}
}
연산 횟수가 3N인 경우
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class 시간복잡도_판별원리2 {
public static void main(String[] args) {
int N = 100000;
int cnt = 0;
for (int i = 0; i < N; i++) {
System.out.println("연산 횟수:" + cnt++);
}
for (int i = 0; i < N; i++) {
System.out.println("연산 횟수:" + cnt++);
}
for (int i = 0; i < N; i++) {
System.out.println("연산 횟수:" + cnt++);
}
}
}
두 예제 코드의 연산 횟수는 3배의 차이가 납니다. 언뜻 생각하면 큰 차이인 것 같지만 코딩 테스트에서는 일반적으로 상수를 무시하므로 두 코드 모두 시간 복잡도는 Ο(n)으로 같습니다.
다음 예제 코드를 확인해 보겠습니다.
연산 횟수가 N²인 경우
1
2
3
4
5
6
7
8
9
10
11
public class 시간복잡도_판별원리3 {
public static void main(String[] args) {
int N = 100000;
int cnt = 0;
for(int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
System.out.println("연산 횟수:" + cnt++);
}
}
}
}
시간 복잡도는 가장 많이 중첩된 반복문을 기준으로 도출하므로 이 코드에서는 이중 for 문이 전체 코드의 시간 복잡도 기준이 됩니다. 만약 일반 for 문이 10개 더 있다 하더라도 도출 원리의 기준 ②에 따라 시간 복잡도의 변화 없이 N²으로 유지됩니다.
이와 같이 자신이 작성한 코드의 시간 복잡도를 도출할 수 있다면 실제 코딩 테스트에서 시간 초과가 발생했을 때 이 원리를 바탕으로 문제가 되는 코드 부분을 도출할 수 있고, 이 부분을 연산에 더욱 효율적인 구조로 수정하는 작업으로 문제를 해결할 수 있습니다.